
#Peg solitaire solve plus
This pruning technique dramatically reduces the size of the search tree and the algorithm runs within seconds (depending on the machine of course). In fact, the solution to any peg solitaire problem actually contains two solutions: the original 'forward' solution plus a hidden 'backward' solution, where the individual jumps are executed in the same direction, but in reverse order (and the starting vacancy and finishing location are swapped). mirrored version of aforementioned stored states. Then at step #3, we restrict the recursive call to only those states that do not coincide with a rotated resp. Peg solitaire describes a general class of peg-jumping games in which a player is initially. Now, the idea is to store each occupation state for which the algorithm already determined no solution can exist. Solving the peg solitaire game using the zChaff SAT Solver. So, for each occupation of stones we have eight states that are equivalent w.r.t to solvability: rotate(0, 90, 180, 270) + mirror(rotate(0, 90, 180, 270)) To see this, by induction we easily can verify that the mirrored moves provide the same state in the mirrored game, either no movement available or solution (one in the center). Similarly, if you mirror the current state of occupation along the vertical center axis, again we would expect the answer if a solution still is possible to remain the same: O O O O O O O X X O O O O O O X O O O O O O O O O O O O O O O O O mirrored: O O O O O O O O O O X X O O O O O X O O O O O O O O O O O O O O O If you look at any occupation state of the stones and you now turn the game clockwise 90 degrees around its center, the answer if this state can lead to any solution remains the same. The idea is to use symmetries of the game. What we can do instead, is to use a very promising pruning technique. This number might be a little overestimated, but it already gives an impression that we can encounter problems.Īnd indeed, implementing the above approach takes hours to solve the problem (on my machine). If we estimate after each move there are two more possible moves available, then this amounts to 2^49 possible paths. In order to remove 49 of them, we need at least 49 moves. The problem though is, for exponential complexity the exponent is already a little too high. Its complexity clearly is exponential since most of the time there will be more than one move available.
#Peg solitaire solve series
This algorithm is the typical approach of trying out all possible series of moves until the solution has been found.

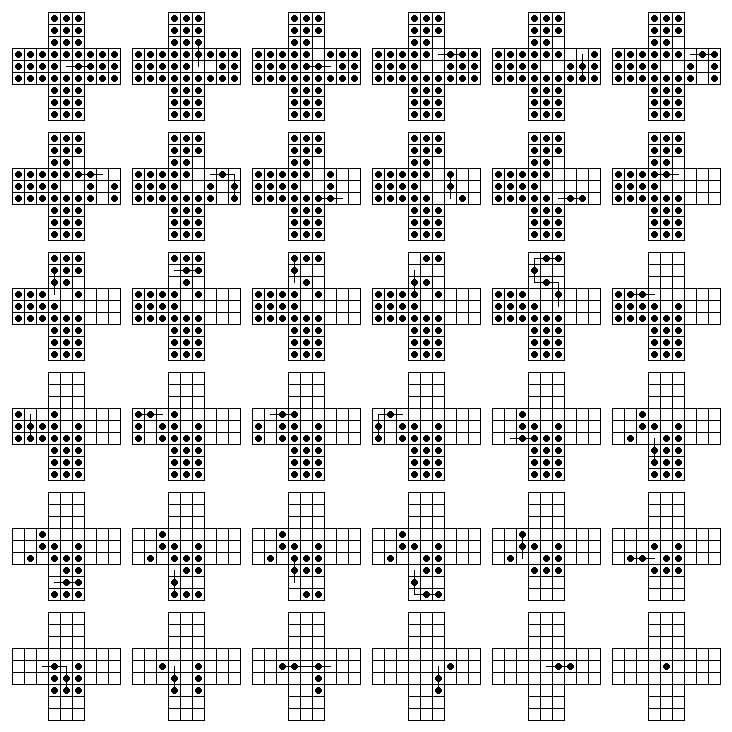

Each time with the resulting new state of occupations, go back to #1. If no possible moves are available, stop the search along this ‘path’. These are those that either vertically or horizontally let jump a stone over another into a non-occupied position and remove the other. Verify if the solution has been attained, that is, only at the center a stone is left over.We start with the initial state where every position except the center is occupied with a stone. The most basic approach is to solve the problem inductively.


 0 kommentar(er)
0 kommentar(er)
